PART 14: VIBRATIONAL MODES OF GUITAR SOUNDBOARD
Because a guitar soundboard is fixed along its edges and has a characteristic waisted shape with a large lower bout, there are only a certain number of ways in which it is free to vibrate. These are called “top modes”, and they are the same in every flat top guitar. Together they produce the sound we recognize as “guitar”[1].
NODES AND ANTINODES
First, some definitions. An object vibrating in a complex way, such as a guitar string, will show points of maximum movement, interspersed with stationary points.
In the case of a guitar string, the fixed point at each end is always a node, but an elastic string can support a number of different modes of vibration. Here is a diagram of the first four possible modes for a guitar string:
This diagram comes from:
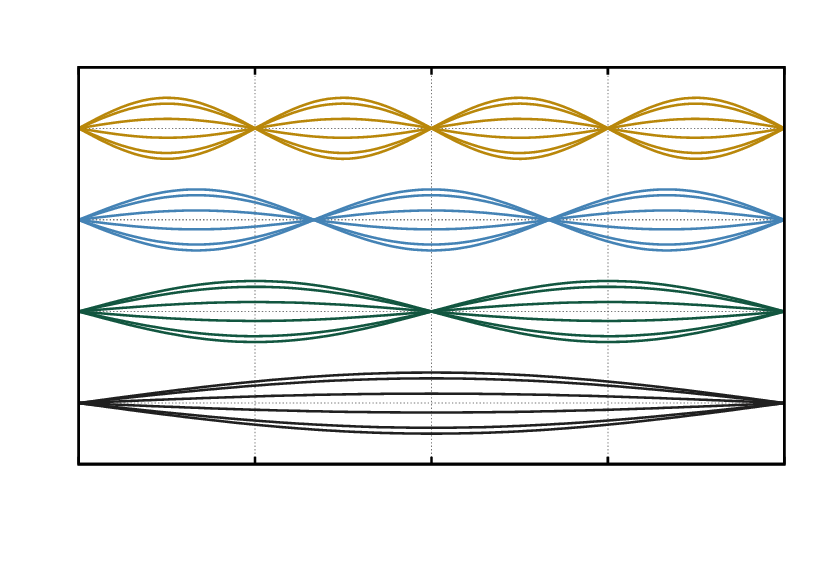
Points of maximum displacement from the string’s rest position (a straight line, of course) – are called antinodes. In the top diagram you can see four antinodes.
Points of no movement are called nodes. In the top diagram the string mode has five nodes.
The bottom picture shows the simplest, or fundamental mode with an node at each end and one antinode in the centre.
The number of antinodes is called the harmonic number n, so here we see n = 1, 2, 3, and 4.
A string has many higher modes available to it when plucked, but the higher the harmonic number the shorter-lived they are. This is why the attack when you pluck a string is vibrant and complex. As the string rings over time, the higher modes die out one by one, eventually leaving the fundamental by itself.
GUITAR TOP MODES OF VIBRATION
Flat top guitar soundboards also show an unvarying pattern in the ways that they are able to vibrate.
The diagrams in this section give a basic idea of how the soundboard of a guitar responds when it resonates at particular frequencies. The + sign indicates the maximum possible upwards deflection from the normal flat surface, and a – sign is a maximum downward deflection.[2]
The dotted line each diagram is the node, the points that stay fixed during the vibration.
What’s important to realise is that all guitars with a flat, relatively thin soundboard show these modes. The main reason why different guitars sound different from each other (different timbre) is that while they all support these same modes they do it to different degrees.
As you look at the diagrams below, you can see how the soundboard bracing can have a huge effect on the guitar’s response.
THE MONOPOLE
The monopole is the simplest vibrational mode, and is associated with the the coupled air-cavity resonance frequency at around 150Hz. The top (and often the back) surface acts like a bellows forcing air in and out of the soundhole. [3]

The top monopole (one antinode), which is the lowest frequency “breathing” mode
It is possible to get a guitar soundbox to blow out a candle by placing the soundhole next to the flame and tapping the bridge firmly. This produces a puff of air that can blow the flame out.
THE CROSS DIPOLE
The cross dipole is a response to higher driving frequencies than the monopole, typically around 300Hz. There are two antinodes (hence “dipole”), and as one is moving up the other is moving down.

The cross dipole (two antinode) mode: each side of the lower bout vibrates separately and out of phase[4]
THE LONG DIPOLE
The long dipole mode is typically found at about 400Hz. Again, there are two opposite-phase antinodes

The long dipole mode, where the two antinodes vibrate out of phase
THE CROSS TRIPOLE
The cross tripole mode is typically found at around 450Hz.

The cross tripole mode, the centre pole out of phase with the two outer ones
These simple diagrams represent only the briefest overview of the top modes, and there a further resonances at higher frequencies with as many as 8 antinodes.
But as for a string, the more complex the mode the shorter-lived it is. One reason a bowed instrument sounds different to a plucked one is that a bow provides a continuous supply of energy to the soundboard, and that tends to prolong the higher modes. The violin’s timbre is more complex than the guitar’s.
THE TOP BOUT
Notice in the diagrams above, the area of the soundboard near the soundhole is pretty inactive. No guitar is as simple as these diagrams, but the top bout area doesn’t contribute a great deal to the guitar’s sound because it is usually heavily braced to withstand the force on the neck trying to make the guitar fold into two.
One potential advantage of the double sound slot geometry is that it may free up more of the upper bout to contribute to the guitar’s sound.
A NOTE OF CAUTION
If you look into this on line, you may come across diagrams showing different and more complex modes derived from Chladni plates. These are metal plates set vibrating by using a violin bow.
The patterns you see from Chladni plates will be different from the ones I’ve just shown simply because a Chladni plate has free edges, whereas a guitar soundboard is connected to the rest of the soundbox all around its edge.
FOOTNOTES
[1]Different guitars have different timbres largely because each instrument has its own particular balance between the top modes produced, both in strength and frequency. The differences are mainly due to the top bracing system used, the mass of the soundboard, its stiffness – and, as we have now seen, by the soundhole geometry.
In my opinion, the material used for the back and sides has only a subtle effect on the sound produced by a guitar, compared with the properties of the soundboard. Many would disagree, and I am happy to concede that others may have a better ear than mine.
[2]These points of maximum displacement from rest in either direction are called “antinodes”.
[3] In fact there are three separate frequencies associated with this mode, as explained by Gore and Gilet (Contemporary Acoustic Guitar Design, P1-82). The reason behind this is beyond a simple description of top modes.
[4]Two oscillators moving in step are “in phase”; if moving in the opposite sense they are “out of phase”. These differences are measured by “phase angle” where a complete cycle of vibration is 360 degrees, half a cycle is 180 degrees, and so on.