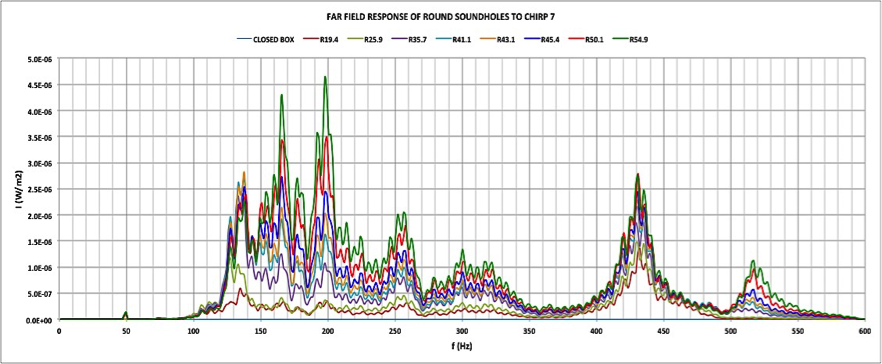
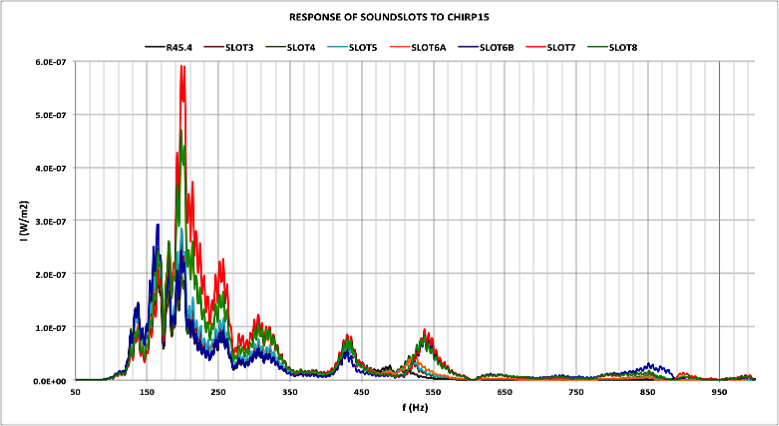
Over the last few years I have been doing research into acoustic guitar resonance, as I’ve reported elsewhere in this blog (see Guitar resonance and soundhole geometry sections).
The research was prompted by an article published in the Proceedings of the Royal Society in 2015 called The evolution of air resonance power efficiency in the violin and its ancestors
http://rspa.royalsocietypublishing.org/content/471/2175/20140905.full
This paper traces and explains the physics behind the evolution of violin family soundhole over 8 centuries leading up to the classical f-hole design we’re familiar with.
I wondered whether the same principles could be used to improve to the modern flat top steel string guitar, so I decided to find out experimentally.
The report of what I found is in the Guitar resonance and soundhole geometry sections on this site.
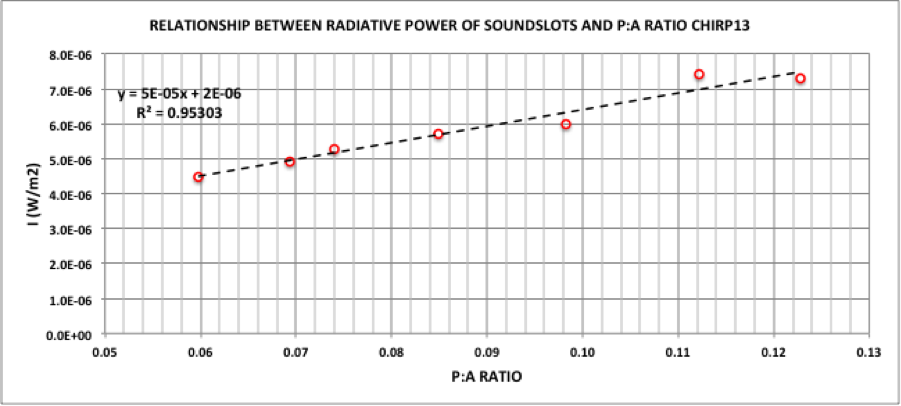
The conclusion I reached is that, as the Royal Society paper suggested, acoustic instruments with long thin soundholes radiate more effectively than traditional round soundholes. The critical factor is the ratio of the soundhole perimeter to its area – the P:A ratio. My research showed significant benefits where the P:A ratio is larger than 0.1m-1 as shown in the diagram below.
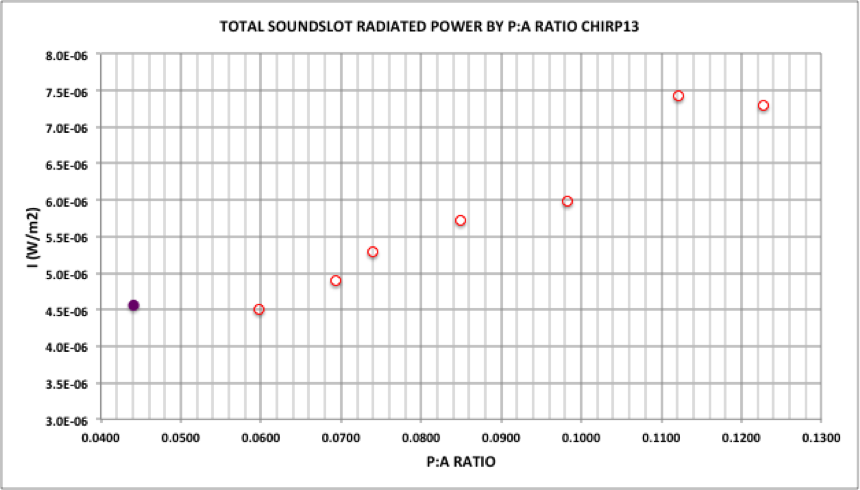
The purple data point shows the total radiative power of a 50mm diameter round soundhole compared to a set of different P:A ratio soundslots.

Diagram 1: Radiative power of high P:A sounslots compared to a traditional round soundhole
It’s clear that above a P:A ratio 0f 0.1 the high P:A slots strongly outperform the traditional round soundhole.
From now on, I’ll refer to high P:A holes as soundslots.
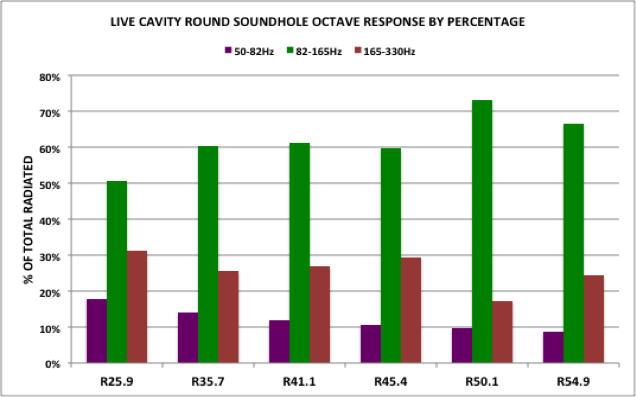
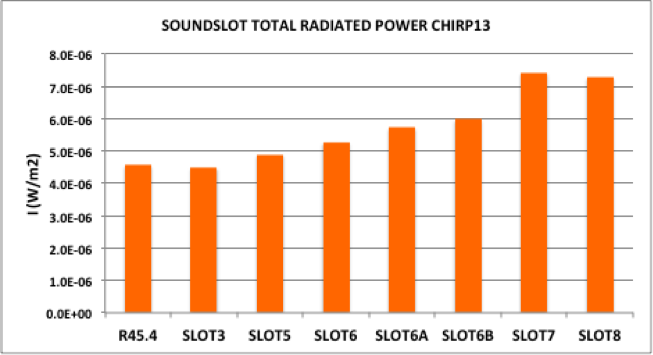
My experiments also showed that the area of a soundhole is important for good projection, something as a guitar builder I had wondered about for a while. As with a lot of acoustic guitar lore, there are many opinions but not much real data.

Diagram 2: Radiative power of different sized round soundholes
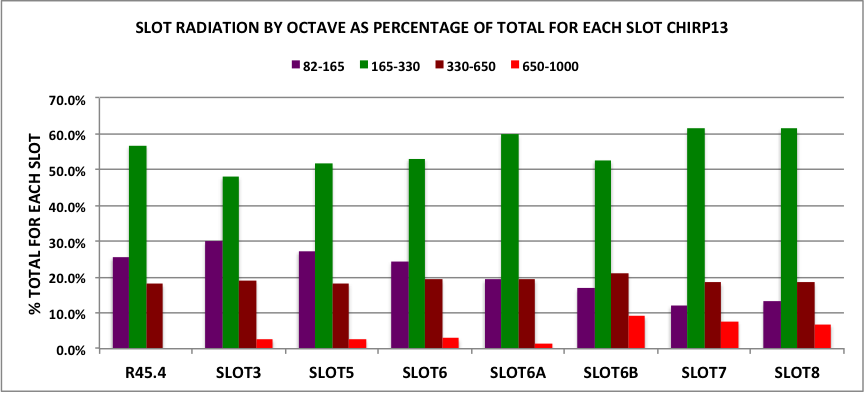
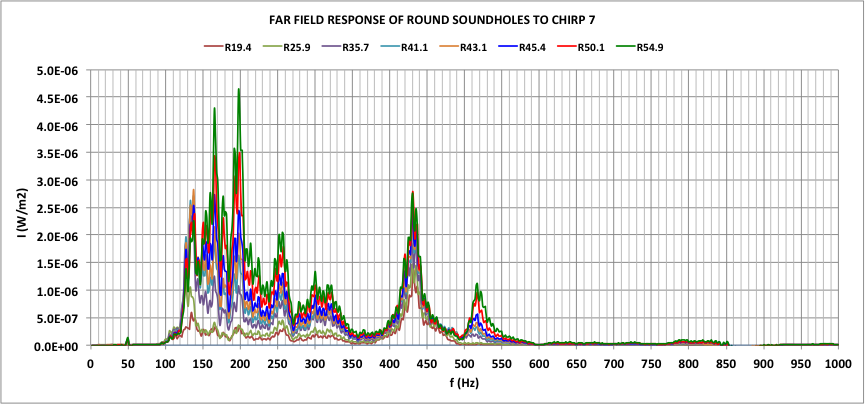
The data shows that the total radiative power of a soundhole increases more or less linearly with the soundhole radius. Bass (purple) and treble (red) response doesn’t vary that much over the frequency range 82 to 1,000Hz, so the increase with area is due to much stronger response in the mid-frequency range (green) as the soundhole size increases.
Larger soundholes are better than smaller ones, it seems, at least until the hole begins to encroach too much on the live area of the soundboard. It would be interesting to know at what point that happens.
But if the area of a soundslot is to be equivalent to a 50mm diameter round hole, the slot needs to be divided in two to be fitted into the top bout of a guitar.
It may be possible to decrease the area of the soundslots in future as the actual performance becomes known, but it made sense to start out with a standard size.
The next picture shows the design I came up with on the right:

Diagram 3: The design of guitars 171 and 172, showing the traditional round soundhole in 171 compared to the soundslots of 172
The experimental data below shows the performance of the double slot design compared with two typically-sized round soundholes (radius 41 and 50mm):

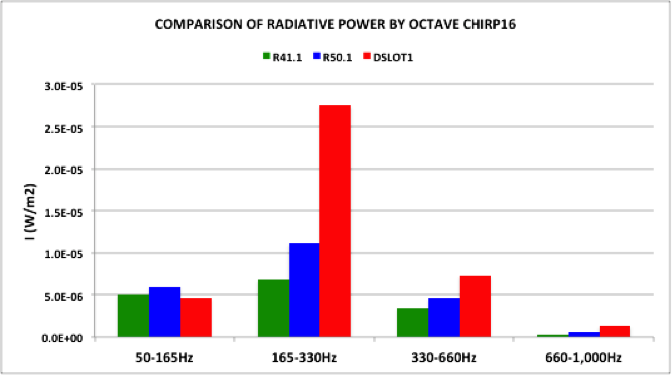
Diagram 4: Total radiative power of high P:A double slot (DSLOT1) compared to two different sizes of round soundhole.
My experiments predict that the double soundslot design will show an increase in radiative power over the 50mm round soundhole of about 80%. This is a rather startling result, but echoes the findings of the Royal Society paper.
Getting into more detail, the diagram below shows that a double soundslot (DSLOT1) strongly outperforms the round soundholes in the 165-330Hz (note E3 to E4) range.

Diagram 5: Performance across 4 octave bands of double soundslot (red) compared to traditional round soundholes (green and blue)
Is the double soundslot design a new idea? Yes and no.
Archtop jazz guitars were built with f-holes before magnetic pickups were available so they would be loud enough to play with swing orchestras. The soundboards of these instruments were usually carved out of a thick wood blank, like a violin top plate, and the f-holes were placed in the same position as a violin relative to the bridge.
The timbre of the archtops was different to the accepted steel-string sound of Martin and Gibson acoustics. The violin family is different to the guitar in that instruments are bowed, giving a steady high-energy input that can sustain a note for as long as the stick-slip action of the bow can be maintained.
Guitars, on the other hand, are plucked instruments with varying but always small ability to sustain an audible note. The archtop jazz guitars needed a rapid, chopped playing style to keep up the volume they needed to be heard over the top of an orchestra. That’s a very different thing to what is needed for the parlour environment in which flat top guitars are usually used.
And the f-hole design isn’t a very suitable arrangement for a flat top guitar with a thin soundboard, because it interferes with the bracing needed to resist string tension. Like the violin family, the carved arched soundboard took much of the string tension load without the need for much extra bracing.
More importantly, f-holes would also change the vibrational modes of the guitar’s lower bout because they rely on the soundboard being firmly connected to the sides of the soundbox. The entire lower bout of a flat top guitar is crucial for the instrument to produce the timbre expected from a modern guitar, and to shift enough air to produce a reasonable volume of sound.
The rationale for the double soundslot flat top design is to increase the responsiveness of the acoustic guitar in its commonly-used context: either as a purely acoustic instrument, or with the use of a microphone in concert.
It seems there would be little benefit to the soundslot design for use with a built-in pickup, but that remains to be seen.
THE AIMS OF THE 171/172 PROJECT
Having gathered the experimental data, the obvious next step is to make a guitar with a high P:A ratio soundhole, both to confirm the experimental result and find out what the effect of the soundhole geometry will have on the guitar’s overall sound. A control instrument with the traditional round soundhole but otherwise identical would also be necessary as a comparison.
The building of two identical-as-possible guitars, one with a round soundhole and one with soundslots is what I am calling the 171/172 Project, referring to the serial numbers of the two guitars to be built.
The two instruments need to have the same area of soundhole. The round hole is 45mm in radius, giving it an area of 6,362mm2, so the high P:A slot has to have the same area. A length of 425mm and a width of 15mm achieves this, but is quite hard to fit into the guitar top without compromising the lower bout tonally and structurally.
The solution was to fit two slots around the edge of the upper bout on either side of the neck.
This should be structurally sound, and has an extra advantage. The normal reinforcement that goes in around a centrally-placed round soundhole tends to deaden the response of the upper bout. With two slots placed at the edge, there is greater potential for the upper bout to remain live over a greater area than with the round hole. What effect this will have tonally is difficult to predict – which is one reason for building the instrument to find out.
This picture shows the design I arrived at for the soundslot geometry for instrument 172:

Diagram 6: 172 soundboard showing carbon-balsa-carbon lattice bracing and soundslots

Diagram 7: 171 soundboard showing carbon-balsa-carbon lattice bracing and round soundhole
I decided the two test instruments would be nylon sting neoclassical guitars.
Not having any great attachment to traditional design and build, I decided to incorporate some other features in the two guitars:
- Using a truss rod in the neck for adjustment of playability and better sustain
- The use of a crude form of side mass-loading (in this case, a 6mm layer of bamboo lining the side of the soundbox (see Gore Contemporary Acoustic Guitar Design and Build Vol 1, 2.3.12.2))
- Using a steel-string style headboard and tuners rather than the classical pierced style (which I find a pain to build and use)
- Using a carbon fibre and balsa laminate for the top bracing, in the form of a lattice rather than the traditional fan bracing
Once the two guitars are complete, I will be investigating their resonance characteristics by tap testing to measure differences is projecting power and timbre.
Timbre, of course, is the more important of the two. How the vibrational modes of the soundboard will form with the new design is unpredictable, particularly with the free edges to the slots in the upper bout.